「ゼロ知識証明とzk-SNARKs」を初心者にもわかりやすく解説！

ビットコインなどの一般的なパブリックチェーンは、ブロックエクスプローラを利用することで、他人のものも含め全てのトランザクションの内容を自由に閲覧することができます。

トランザクションの内容には送金者と受取人のパブリックキー(ウォレットアドレス)や送金額なども載っているため、特定のウォレットの資産の行き先などを追跡することができてしまいます。

こういった特徴は分散型台帳の大事な要素である一方、「誰がどこにいくら送ったか」がわかってしまうことに不便さを感じることも確かです。

そこで昨年から注目されているのが、「ゼロ知識証明」というコンセプトを基にしたzk-SNARKsというテクノロジーです。

同テクノロジーを利用したブロックチェーンでは、「トランザクションが正当に行われた」という情報を一般に開示する代わりに、上記のような取引内容を完璧に隠すことができます。

こちらのページでは、そのゼロ知識証明とzk-SNARKsとはいったいどのような仕組みなのかを、初心者にもわかりやすく丁寧に解説していきたいと思います。

ゼロ知識証明とは

ゼロ知識証明とは1985年に初めて定式化されたコンセプトで、証明者(prover)と検証者(verifier)の二者間で行われるある「対話」を意味します。

この対話では、証明者がある秘密を知っていることをその秘密の内容を明かさずに検証者に証明します。

数学的には「命題が真であることを、それ以外の情報を与えずに証明する」といいます。

このコンセプトは、分散型ネットワークのプライバシーを保つ上でとても役立つもので、zk-SNARKsと呼ばれる応用型がZCashやQuorumなどのブロックチェーンで利用されています。

ジャン＝ジャックの洞窟

ゼロ知識証明を簡潔に説明できる例として、ベルギーの暗号学者・ジャン＝ジャック・キスケタが提案した「洞窟の問題」があります。

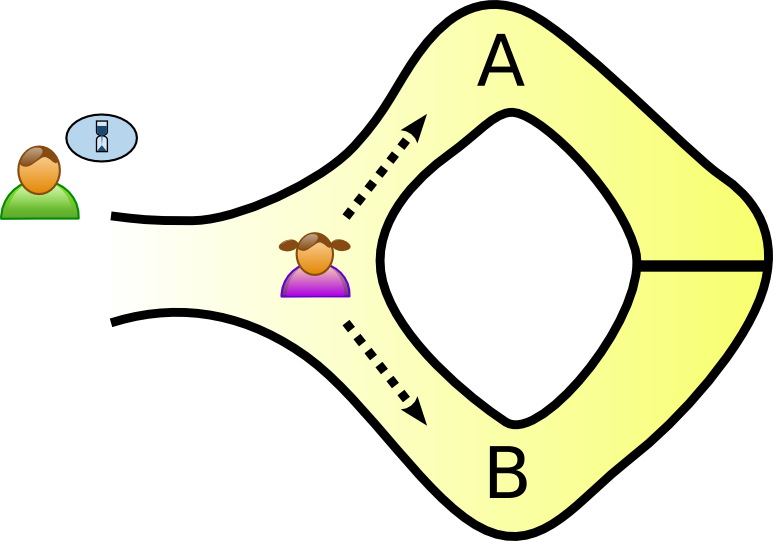
ウィキペディアより

この例では、ピンク色の服を着た証明者Pさんが、緑色の服を着た検証者Qさんに、 上図のような洞窟の最奥部にある扉を開けるパスワードを知っていることを証明します。

Pさんは洞窟の入り口で、最奥部に到達するルートAまたはBをランダムに選んで進んでいきます。ここでは、PさんはルートAを選んだものと仮定します。

Pさんが最奥部に到達するまで充分な時間が経過した時点で、洞窟の外で待機していたQさんがルートAまたはBをランダムに選び(中へは進まない)、Pさんに選ばれたルートから戻ってくるように叫びます。

ルートAとBを仕切る扉のパスワードを知っているPさんは、ルートAから戻るように言われれば来た道を戻ることができ、ルートBが選ばれたケースでは扉を解錠してBから戻ることができます。

この作業を何度か繰り返して、Pさんが毎回正しいルートから帰ってくれば、QさんはPさんが本当にパスワードを知っているということを、パスワード自体を知ることなく確認できます。

ノンインタラクティブ型

ゼロ知識証明の例をもう一つ挙げます。こちらは、「ノンインタラクティブ型」と言われるタイプの証明になります。

証明者Xさんは、5点満点のテストで「Yさんと同点ではないこと」を検証者Yさんに証明します。ここでは、Xさんは5点、Yさんは3点を取ったと仮定します。

まずXさんは、5つの施錠された箱を用意します。それぞれの箱には1点、2点、3点、4点、5点と点数がふられています。

Xさんはそれぞれの箱の鍵をYさんに渡し、部屋を退出します。退出を確認したYさん(検証者)は、自分の点数(3点)以外の箱の鍵(1, 2, 4, 5点)をその場で捨てます。作業が終わると、Yさんは退出します。

今度はXさんが、自分の点数が書かれた箱(5点)の蓋の隙間から丸印のついた紙切れを入れ、それ以外の箱(1, 2, 3, 4点)にバツ印のついた紙切れ滑り込ませます。

再度XさんとYさんが部屋を入れ替わり、Yさんは鍵を使って3点の箱を開けます。中に入っている紙切れは必然的にバツ印であることから、YさんはXさんと同点ではないことがわかります。

しかし、Yさんは、Xさんの点数が自分より良かったのか、悪かったのかはわかりません。

この例は、洞窟の問題と違い、XさんとYさんの直接のやり取りを必要としません。このようなゼロ知識証明を「ノンインタラクティブ型」と呼びます。

ゼロ知識証明のルール

ゼロ知識証明には、証明者による不正を最小限に抑えるために守るべきルールが定義されています。

ひとつめは、完全性(completeness)と呼ばれるものです。これは「証明者が秘密を持っていることが本当ならば、検証者はそれが本当であることが必ずわかること」を意味します。

例えば、洞窟の問題では、証明者Pさんがパスワードを知っているなら、検証者QさんはルートA、Bをランダムに選ぶ作業を繰り返すことででPさんが本当にパスワードを知っていることを確認できます。

ふたつめは、健全性(soundness)と呼ばれ、「証明者が秘密を持っているという嘘をついている場合、検証者は高確率でその嘘を見抜ける」というものです。

洞窟の問題で証明者Pさんが嘘をついていた場合、Pさんは最奥部の扉を解錠できないため、来た道(上記の例ではルートA)から戻るほかに選択肢がありません。

検証者Qさんがランダムに選ぶルートがAである確率は50%であることから、この作業を繰り返していけば、Qさんが毎回Pさんによって選ばれたルートから戻ってくる確率は極端に低くなります。

証明の回数を重ねるごとに証明者Pさんが不正を働ける確率が低くなるため、QさんはPさんが嘘をついていることを高確率で見抜ける、ということになります。

最後に、ゼロ知識証明はゼロ知識性(zero-knowledge)というものを満たさなければなりません。これは、検証者が証明の結果得られる知識は、証明者の命題が真であることのみであるという意味です。

洞窟の例では、検証者は証明者がパスワードを知っていること(命題)が本当であることは確認できますが、そのパスワード自体を知ることはできません。

zk-SNARKsとは？

匿名性の高いことで有名な暗号通貨・ZCashなどは、zk-SNARKs(ゼットケー・スナーク)と呼ばれるゼロ知識証明の応用型をトランザクションの記録に利用しています。

ZCashでは、第三者が得られる情報は「トランザクションが正当に行われた」という命題が真であることのみで、送金者や受取人、送金額などといった情報は確認できません。

zk-SNARKsのzkはZero-Knowledge(ゼロ知識)を意味し、SNARKはそれぞれ以下の略称となっています。

• Succinct (簡潔) – 証明結果は証明のプロセス(計算)に比べサイズが軽い。証明プロセスをノンインタラクティブ型にすることで、証明結果の容量を節約できる。
• Non-interactive (ノンインタラクティブ) – トランザクションの正当性を確認したい検証者が、証明者と直接やり取りせずに証明を確認できる。
• ARgument – 証明者の計算能力には限りがある。並外れた計算能力を持つ証明者は、力づくで暗号を解き、虚偽の証明を提出できてしまう。
• of Knowledge – 証明者は、取引に関与するウォレットのアドレスなどといった知識を前もって知っていない限り、証明を作成することはできない。

証明が簡潔かつノンインタラクティブ(証明者から検証者へメッセージを送るだけ)であることで、ブロックチェーン上に記録する内容を少なく抑えることができる、ということになります。

Argument of Knowledgeは、zk-SNARKsが満たすべき仮定、と考えることができます。

zk-SNARKsはZCash以外にも、米JPモーガンのQuorumでも実装されているほか、イーサリアムでも実装を検討していることがわかっています。

【ゼロ知識証明】プライバシー銘柄「zCloak Network」とは？テストネットのやり方も解説

まとめ

ゼロ知識証明とzk-SNARKsについて、大事な点をもう一度確認しておきましょう。

ZCashによるzk-SNARKsの解説はコチラからアクセスできます。また、ゼロ知識証明のより数学的な解説はコチラに載っています。